√完了しました! exp x 2 積分 181877-Exp(-x^2)*cos(x) 積分
09 年度物理数学II 宿題(11 月2 日出題、9 日提出) 解答 担当吉森明 問題1(1) 図のような積分路Cで R C exp−z2dz を計算することでR ∞ −∞ exp−x2cos(2bx)dx を求めよ。(2) 前回演習の問題No4II(c)~(g) をやりなさい。 解答 (1) a) exp−z2 は全複素平面内で正則なので、積分路をC とするD dx x 2n1exp("ax)=(2n1)x2nexp("ax2)"2ax2nexp=exp("ax 2 0 # $)dx= 1 2 % a である. 関連する定積分 マクスウェルボルツマンの速度分布式から平均エネルギー などを計算するには次の積分が必要である: !
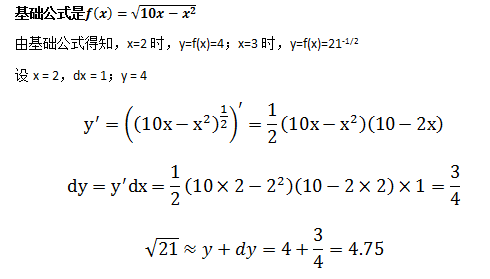
单变量微积分笔记11 微分和不定积分 我是8位的 博客园
Exp(-x^2)*cos(x) 積分
Exp(-x^2)*cos(x) 積分-21/6/09 · 多分、初等関数で表すことはできないと思います。 部分積分で次数を減らしてみましょう。 ∫x^2*exp(x^2)dx=∫(x/2)*(2x*exp(x^2))dx=(x/2)*exp(x^2)∫(1/2)exp(x^2)dx (2x*exp(x^2)=(exp(x^2))')となりますが、∫exp(x^2)dxは初等関数で表すことができないと記憶しています。 通報する 共感・感謝の気持ちを伝えよう! ありがとう(OKチップをおくる) 1 関連するQ&A ∫exp(x)/x dxの積分28/6/08 · e^(x^2)の原始関数を初等関数で表すことは出来ません。 高校までの知識では積分できないと言うことです。 積分範囲を0,∞とすれば定積分は計算でき ∫0,∞{exp(x^2)}dx = (√π)/2 となります。 これは大学2年くらいの知識があれば証明できます。



E的x次方积分 万图壁纸网
6/3/21 · e − a x 2 e^{ax^2} e − a x 2 は偶関数なので積分値が半分になっています。 ガウス積分で,被積分関数に x x x や x 2 x^2 x 2 をかけたものも見かけます: ∫ 0 ∞ x e − a x 2 d x = 1 2 a \displaystyle\int_0^{\infty}xe^{ax^2}dx=\dfrac{1}{2a} ∫ 0 ∞ x e − a x 2 d x = 2 a 1不定積分(まとめ2) 不定積分の漸化式 → 携帯版は別頁 指数関数,対数関数の不定積分 (個別に置換積分,部分積分を要しない問題だけ) ≪公式≫ 指数関数の不定積分 ∫wn e x dx=e x C (1) ( e=2Exp_積分_x^2,積分,積分,積分,積分,exp(ax^2),積分 exp_積分_x^2 の商品検索結果 女性のためのヘアケア、女性用育毛剤・育毛シャンプーに関する話題や情報
よく使う積分の公式 ∫ xndx = 1 n1 xn1 C ∫ x n d x = 1 n 1 x n 1 C (n ≠−1) ( n ≠ − 1) ※基本中の基本! ∫ eaxdx = 1 a eax C ∫ e a x d x = 1 a e a x C ( a a は定数) x C ※基本中の基本! x C ※基本中の基本! ※ C C は積分定数です。6/3/21 · 部分積分を2回繰り返すことにより, ∫ x 2 e x d x = x 2 e x − 2 x e x 2 e x C \displaystyle\int x^2e^xdx=x^2e^x2xe^x2e^xC ∫ x 2 e x d x = x 2 e x − 2 x e x 2 e x C であることが分かる。計算の過程は瞬間部分積分の記事参照。∫ex 2 dxという関数は解析的には解けません。 こういうときにExcelが役立ちます。 01刻みでxを用意して、=exp(b4^2))で関数を計算します。 これはこんな関数です。 これを0から05まで積分してみましょう。 xは01刻みなので、01×高さで長方形の面積を作ります。
J n =x 2nexp("ax2 0 # $)dx ただしa > 0とする.x2n1exp(–ax2)を微分すると !この漸化式をもとに, ∫ x 3 e x d x の積分を計算してみる. I 0 = ∫ x 0 e x d x = ∫ e x d x = e x I 1 = x 1 e x − 1 · I 0 = x e x − e x = (x − 1) e x I 2 = x 2 e x − 2 I 1 = x 2 e x − 2 (x − 1) e x = (x 2 − 2 x 2) e x I 3 = x 3 e x − 3 I 2 = x 3 e x − 3 (x 2 − 2 x 2) e x = (x 3 − 3 x 2 6 x − 6) e x のように, I 0 , I 1 , I 2 , I 3 と順次漸化式を利用して計算するとよい.Exp(ix^2)のガウス積分 home> 物理数学> このページのPDF版 サイトマップ ファインマンの経路積分で何気なく使っていたので,確かめてみました.短いです. と置きます. すると,収束因子として, を用いて, となり,よって, ですね.なるほど, ですから,この に を代入したものに一致す



从 E X Sinxdx出发 积分随想 I 知乎



不定积分的解题思路及技巧总结 知乎
(%e^(x^2) または exp(x^2) を微分する。) 積分 Maxima では不定積分、定積分が計算できます。 積分定数は表示されないので注意してください。 また、うまく計算できないこともあります。 integrate(f(x), x) 不定積分 integrate(f(x), x, a, b) 区間 a, b の定積分含有a 2 − x 2 ( a 2 > x 2 ) {\displaystyle {\sqrt {a^ {2}x^ {2}}}\qquad (a^ {2}>x^ {2})}的積分 ∫ a 2 − x 2 d x = 1 2 x a 2 − x 2 a 2 2 arcsin x a C {\displaystyle \int {\sqrt {a^ {2}x^ {2}}} {\mbox {d}}x= {\frac {1} {2}}x {\sqrt {a^ {2}x^ {2}}} {\frac {a^ {2}} {2}}\arcsin {\frac {x} {a}}C}∫ 2 0 xexdx = xex2 0 ∫ 2 0 exdx = 2e 2 ex 0 = 2e2 e2 1 = e2 1 例52 次に, ∫ logxdx を部分積分法を使い求めよう. ∫ logxdx = ∫ 1 logxdx = ∫ (x)′ logxdx = xlogx ∫ x 1 x dx = xlogx ∫ dx = xlogx xC 計算練習3 次の定積分と不定積分を求めなさい. 1 ∫ 1 0 (x x3)dx 1 4 2 ∫ 1 0 e2xdx




高斯積分 積分e X 2 中文版 Gaussian Integral Integral Of E X 2 Youtube
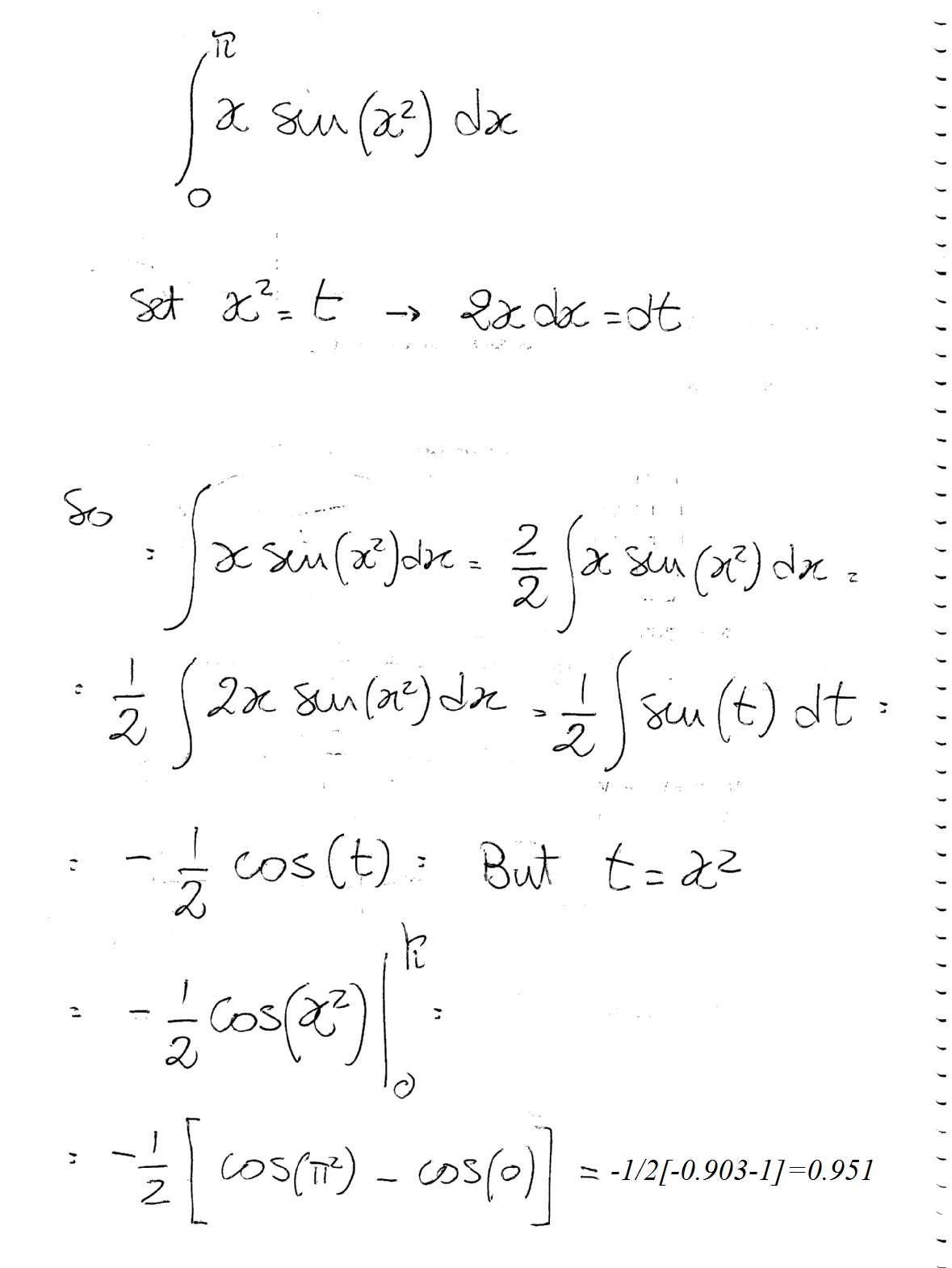



How Do You Use Substitution To Integrate Xsin X 2 Dx From 0 Pi Socratic
4/6/18 · ガウス積分まわりの公式リスト 具体例で学ぶ数学 ガウス積分に関連する積分公式を整理しました。 e^ {ax^2}や、x^ne^ {ax^2}などの定積分です。 「平行移動しても定 積分 の値は変わりません。 」 「exp第1項に含まれる ダンピング ? 的な何かは、どちら以下是部分指數函數的積分表 ∫ e c x d x = 1 c e c x {\displaystyle \int e^ {cx}\;dx= {\frac {1} {c}}e^ {cx}} ∫ a c x d x = 1 c ln a a c x ( a > 0 , a ≠ 1 ) {\displaystyle \int a^ {cx}\;dx= {\frac {1} {c\ln a}}a^ {cx}\qquad \qquad {\mbox { (}}a>0, {\mbox { }}a\neq 1 {\mbox {)}}}Gaussian exp(x2)のR上の積分値 ∫∞ −∞ exp(2x)dx = p π の導出法について考える。先ずは同値な積分形に書換えて置こう。 命題1. 次は同値である。 (1) ∫∞ −∞ exp(x2)dx = p π (2) ∫∞ 0 exp(x2)dx = p π 2 (3) ∫∞ 0 e−t 1 p t dt = p π (4) 任意のa > 0に対し ∫∞ −∞ exp(ax2)dx = √ π a (5) 任意のa > 0に



Http Tyr0 Chem Wsu Edu Kipeters Chem332 Resources Tableofusefulintegrals Pdf




既有e X又有sinx或cosx的积分题的解法 Weixin 的博客 Csdn博客
(12) 結局目的の積分は I0 = 1 2 √ π a (13) 積分範囲が(−∞,∞) であるときは,被積分関数が偶関数なので,積分はI0 の2 倍になる。 23 xne−ax2 の積分 次のように置くことにする。 In = ∫∞ 0 (14) xne−ax2dx これを部分積分してみる。 In = ∫∞ 0 (15) x(nFresnel 積分の計算 ∫ ∞ −∞ cos(x2)dx =∫ ∞ −∞ sin(x2)dx =√ π 2 あるいは ∫ ∞ −∞ expix2dx =√ πi = √ π 2 (1i) 証明 複素積分をつかう I = ∫ C expiz2dzを考える\begin{alignat}{2} &(1) \displaystyle\int_0^{\infty} \left(\frac{1}{1x^{2^n}}\frac{1}{1x^{2^m}}\right)\frac{1}{x}dx=0\\ &(2) \displaystyle\int_0^{\infty} \left




Matlab 在教学中的应用 Ppt Download



估计积分的值 4 S 0 2 E X 2 X Dx 数学竞赛平台 数学帮 Math110
3 You can write the integral in this form d / d a ∫ exp ( − a x 2) d x And we know that ∫ exp ( − a x 2) d x = π / a被積分関数は f (x, y) = exp(xy)、 積分範囲はx, y ともに 0~1 とする。 (このとき、積分の理論値は (e 1) 2 となる。) 以下のプログラム例は、上記の仕様を満たそうと書きはじめたものである。 ただし、未完成である。110 第 6 章 複素積分の応用 図 64 例 43 の積分路 C 2 故に I = 1 2i 2 i e a 2 e a (618) f (x) は実軸上の区間 a;



1



从 E X Sinxdx出发 积分随想 I 知乎
· ベストアンサー:x^3・e^x^2 を (x^2)・(xe^x^2) とみて部分積分(左を微分,右を積分)して計算すれば ∫x^3・e^x^2 dx=(x^2 1)・(e^x^2)/ 2 高校数学2:y軸として、exp(x^2)を作る 3:y軸を台形積分するための関数を入力する 4:積分結果がどの程度正しいかを評価する といった順で解説します。 まずは左図のように入力します。 ここでx0とdxはx軸を作るためのパラメータで、x=x0m*dx(mは正の整数)となり指数関数 \(e^{x^2}\) は正規分布(ガウス分布)の確率密度関数を表わすのに使用されますが,その不定積分 \(\int e^{x^2}dx\) は初等関数では表わせません.しかし,ゼロから無限大まで積分すると \(\frac{\sqrt{\pi}}{2}\) になることは次のようにして導きます (数学的には厳密ではないかも知れません)




求不定积分xe X 1 X 2 Dx 雨露学习互助




What Is The Integral Of 1 1 X 2 Quora
· 5x^nがかかっているケース(x^n e^{ax^2}) これを の関数と見て微分すると、 となる。 3,4を見るとわかるとおり、この積分は が偶数か奇数かで振る舞いが変わる。 3が 、4が に相当するので、その結果を で微分することによって具体的な の値に対して答えが得られる。ミニクイズexp(x^2)の積分 exp(x^2)の∞から∞までの定積分は? ① 1 ② π ③ π^(1/2) ④ どれでもない 正解 正解は「 ③ π^(1/2) 」 標準正規分布の確率密度関数の変数変換でもいいですし、座標製麺の2重積分の極座標変換でもできます。積分する関数を入力してください 変数 始点 終点 被積分関数 exp (x^2) を次の変数で微分する x 100から100への間隔で = グラフを描く LaTeXエディタで編集 このページへの直接のリンク 定積分の計算 ある区間で定義された関数の定積分を数値
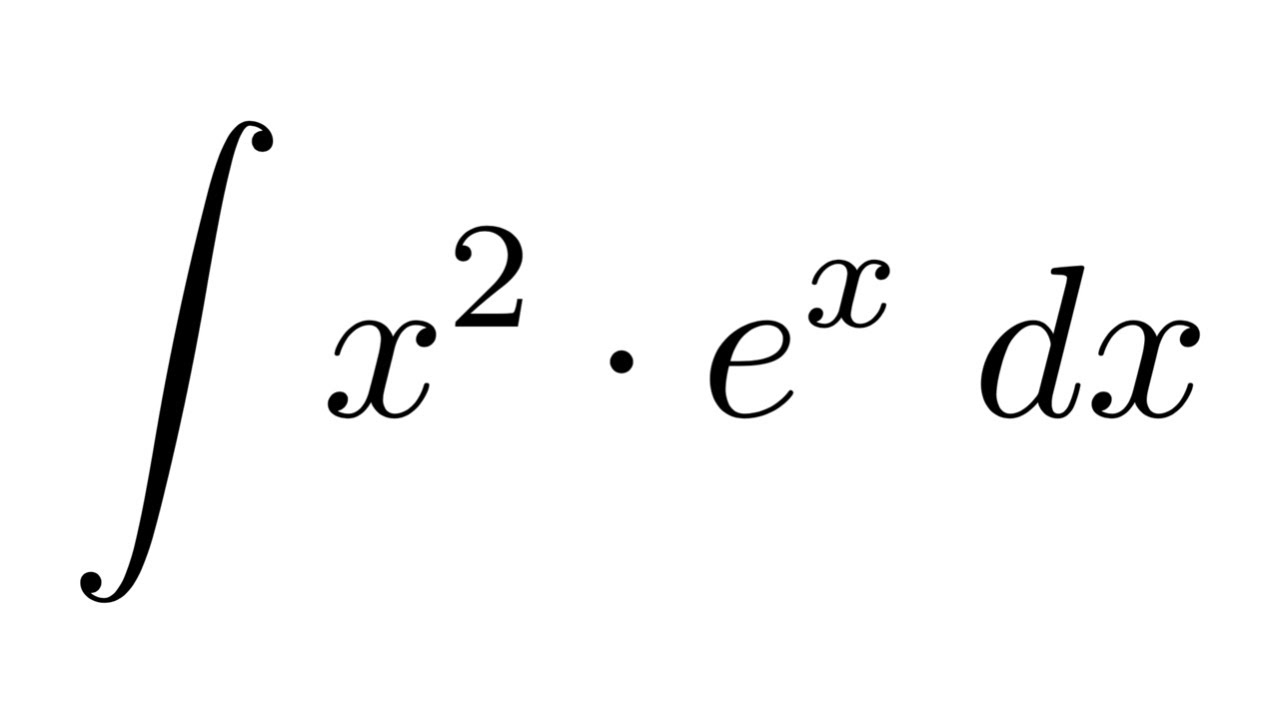



Integral Of X 2 E X By Parts Youtube




一道高数题设 A 1 求积分f A X A E X Dx的最大值那个其中是e的x次方我不知怎么打 雨露学习互助
ガウス積分 ガウス積分とは,つぎのような式で書かれる積分のことです. I = ∫ ∞ −∞ e−ax2dx (1) ここでx は実数,a は正の定数です. ガウス積分の公式 ふつうガウス積分は,公式として扱われることが多いです.ガウス積分の公式はつぎのようなも のです. ∫ ∞ −∞被積分関数 x*exp (x^2) を次の変数で微分する x %e^x^2/2∫∫ D √ a2 y2 dxdy= ∫a a dy ∫p a2 y2 p a2 y2 √ a2 y2 dx ∫a a √ a2 y2 xp a2 y2 p a2 y2 dy = 2 ∫a a (a2 y2)dy= 2a2y 1 3 y3a a = 8 3 a3 a a x= √ a2 y2 x= √ a2 y2 問2 次の累次積分の積分領域を必要な数値を記入して図示した後,積分順序を交換せよ。



从 E X Sinxdx出发 积分随想 I 知乎




定積分 Int Frac 1 1 E X Dx
2 2 x ( ik a 2) =0 である。第 1 項のガウス積分は (Z 1 1 dxe a 1 2 2 x) 2 = dxdy e ( y) =2 0 dr r e r = Z 1 0 dte a 1 2 2 t a 2 より Z 1 1 dxe a 1 2 2 x = p a である。したがって Z 1 1 dxe a 1 2 2 (x ik a) = p a である。これを (611) に代入してフーリエ変換は F (k)= 1 a p 2 exp(k 2 2) (6 12) と積分 e^(x^2) 從負無窮到正無窮, Gaussian integral, integral of e^(x^2) from inf to inf, sqrt(pi), sqrt(π),blackpenredpen, math for fun積分 {e^ (2x)}sinx ∫ e2xsinxdx ∫ e 2 x sin x d x の積分を 部分積分法 を用いて計算する. ∫ e2xsinxdx = ∫ (1 2e2x)′ sinxdx = 1 2e2xsinx−∫ 1 2e2x(sinx)′dx = 1 2e2xsinx−∫ 1 2e2xcosxdx = 1 2e2xsinx− 1 2 ∫ e2xcosxdx ・・・・・・(1) ∫ e 2 x sin x d x = ∫ ( 1 2 e 2 x) ′ sin x d x = 1 2 e 2 x




高斯积分 维基百科 自由的百科全书



计算二重积分ss D E X 2 Y 2 N Sin X 2 Y 2 Dxdy 其中积分域d X Y X 2 Y 2 P 数学竞赛平台 数学帮 Math110
複素積分(2) 問題1 複素積分を用いて, ∫ 2π 0 dθ 4cosθ 5 を求めよ. 解C z = eiθ(0 ≤ θ ≤ 2π) とする. ∫ C f(z)dz = ∫ 2π 0 dθ 4cosθ 5 (1) とおき,これを満たすf(z) を以下で見つける. ∫ C f(z)dz = ∫ 2π 0 f(z) dz dθ dθ = ∫ 2π 0 f(z)ieiθdθ = ∫ 2π 0 f(z)izdθ 一方 1 4cosθ 5 1G'= 1 → g= x (多項式を積分する側に選ぶのは、 相手が対数のときの例外) ∫wn log x · 1 dx = log x · x − ∫wn 1xn x C=x log x−xC ※ ∫wn(多項式) log xdx, ∫wn(指数関数) log xdx ∫wn(三角関数) log xdx 、などにおいては「 log x を微分する側に選ぶ( g= log x とおく)」とスムーズに計算できる。 逆に選べば( f'= log x とおくと) f すなわち log x の不定積分が必要となりB 内の特異点 c を除いて連続であるとする。
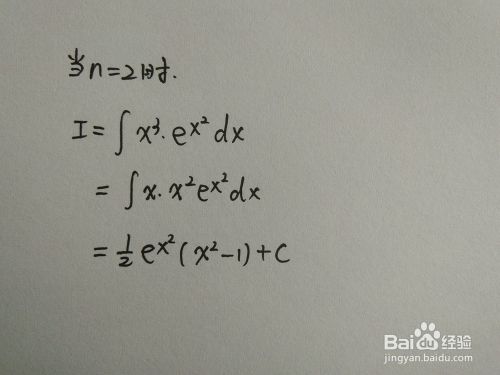



如何求形如 X 2n 1 E X N Dx的不定积分 百度经验




高数之微积分 Dx E X E X 需要详解 雨露学习互助
· まず、 I = ∫ π 2 0 ex sinxdx J = ∫ π 2 0 ex cosxdx I = ∫ 0 π 2 e x sin x d x J = ∫ 0 π 2 e x cos x d x とおきましょう。 先ほどの計算と同じようにして、 I I に対して部分積分を行うと I = eπ 2 − J I = e π 2 − J となることがわかります。 また、 J J に対して
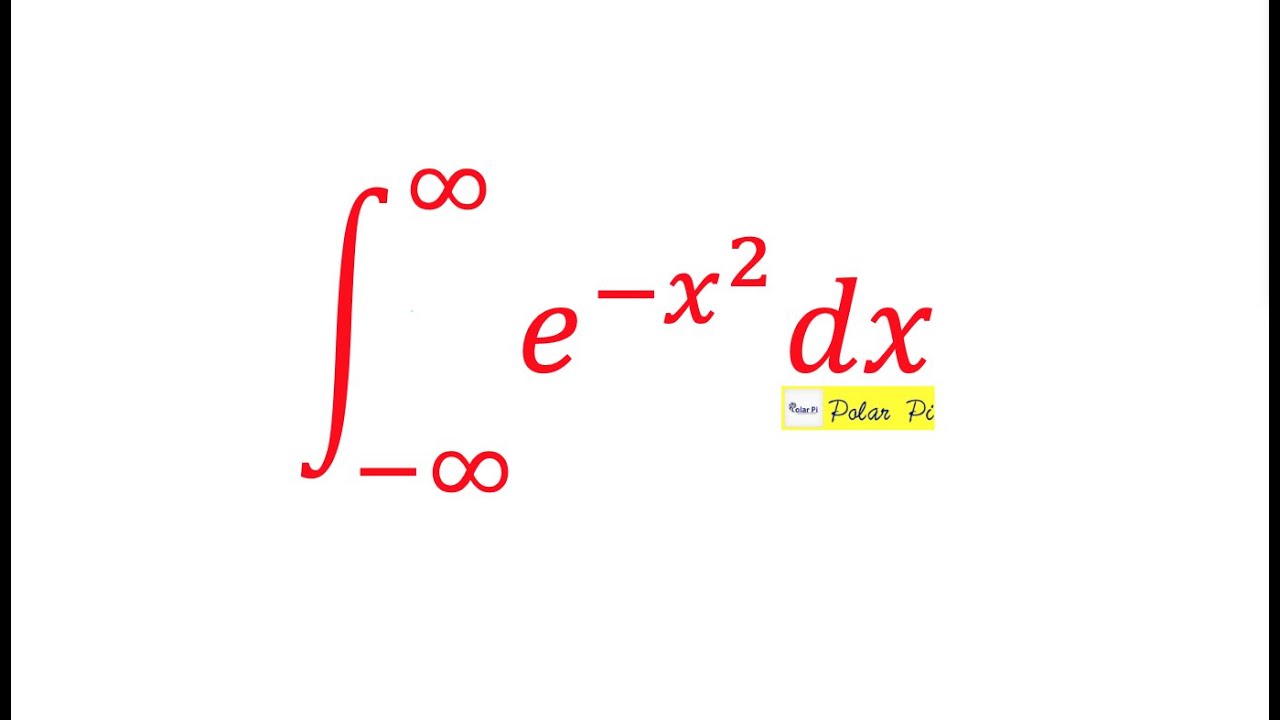



Integral Of Exp X 2 Gaussian Integral Trick Youtube



X 2 E 2x的积分怎么求 数学作业 解题作业帮




Gaussian Integral Wikipedia




ガウス積分の公式集 証明付 理数アラカルト
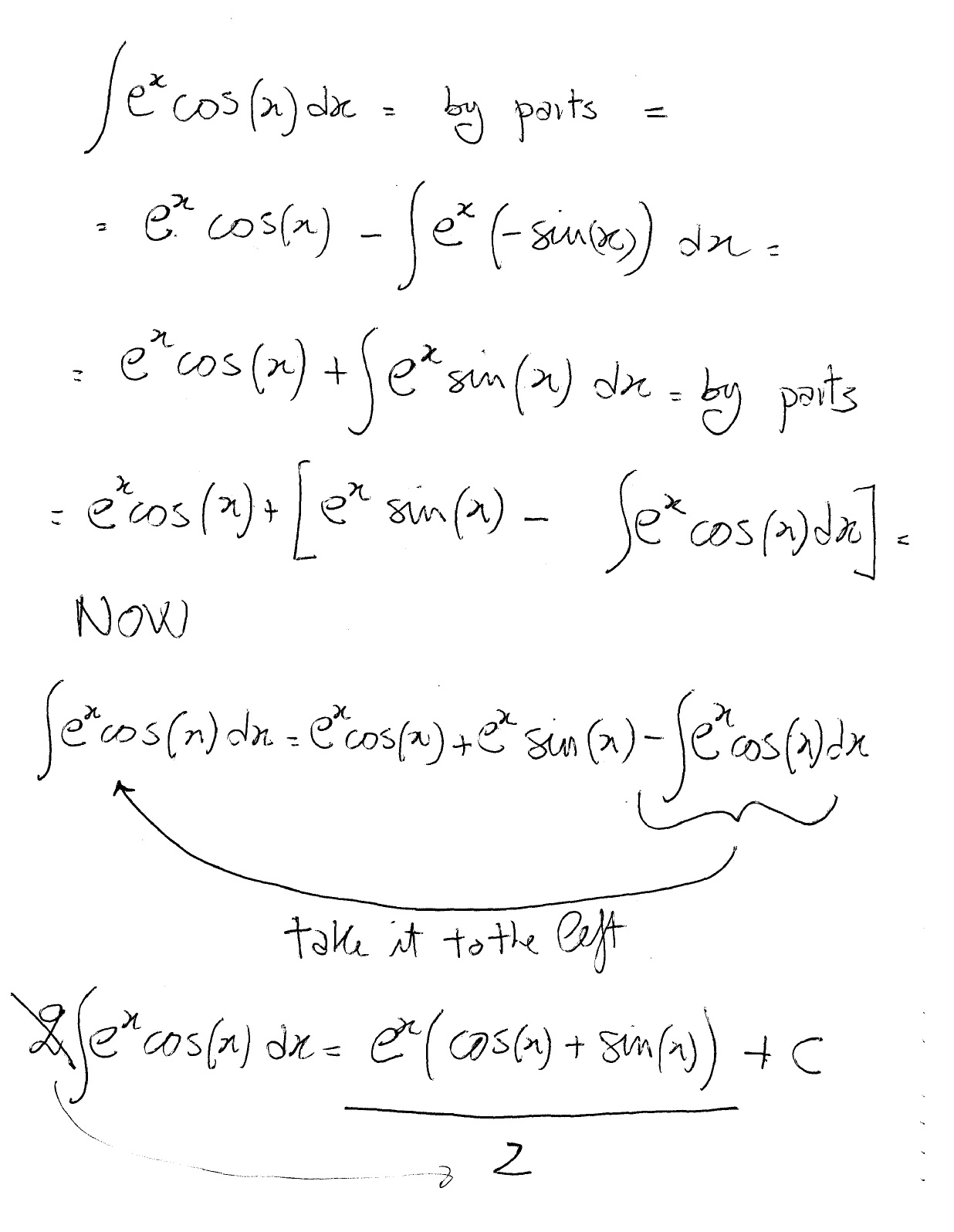



How Do You Find The Integral Of E X Cosx Dx Socratic
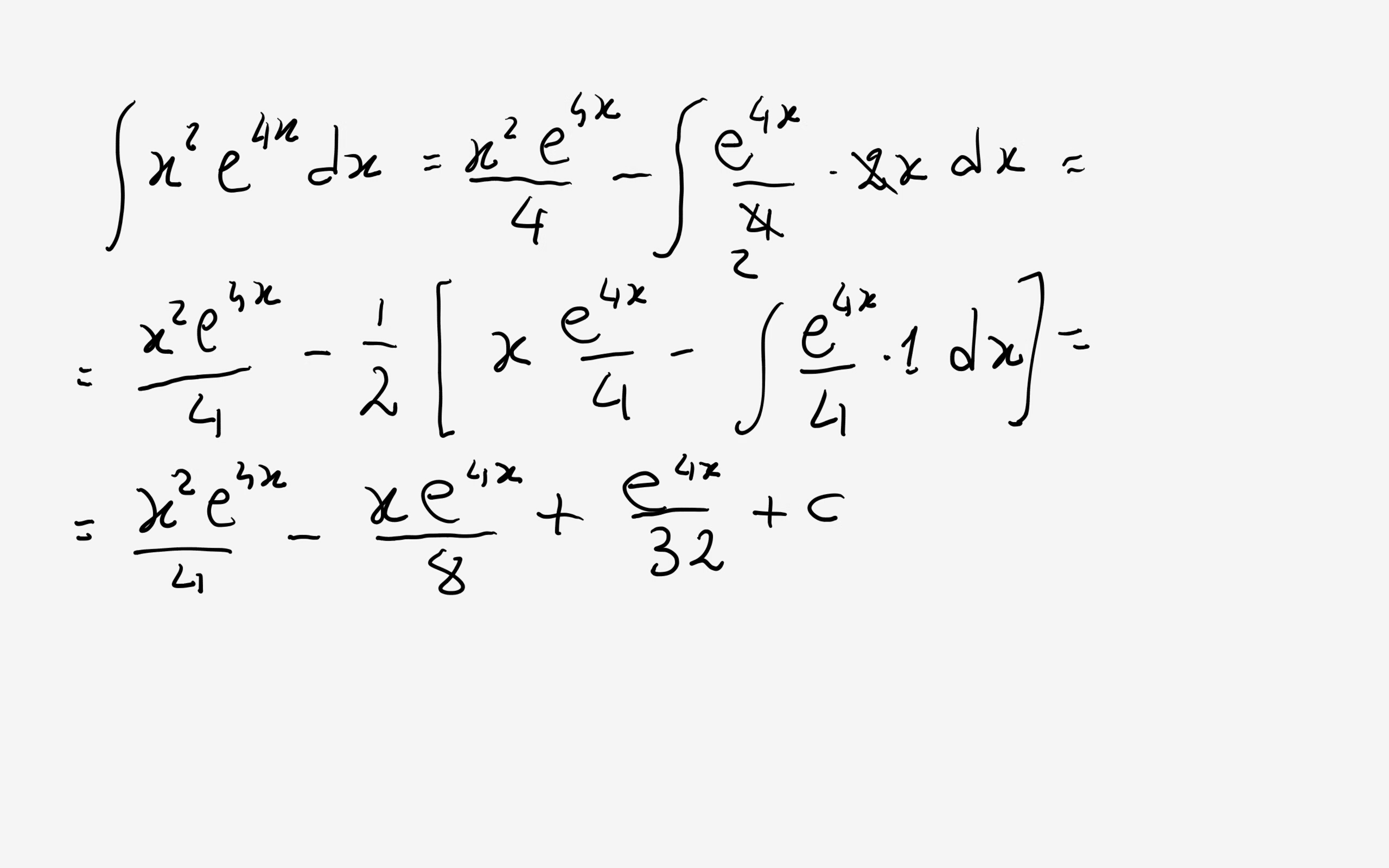



How Do You Integrate X 2 E 4x Dx Socratic




How To Integrate X 3 E X 2 Using Integration By Parts Youtube



Search Q E E7 8d E5 86 Tbm Isch




ガウス積分の公式集 証明付 理数アラカルト




X2ex积分 求不定积分 E X 47 X 2 Dx 三人行教育网 Www 3rxing Org
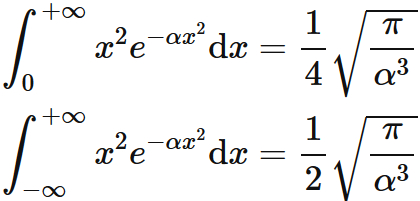



Gaussian Integral Formula And Proof Semath Info




Gaussian Integral Wikipedia
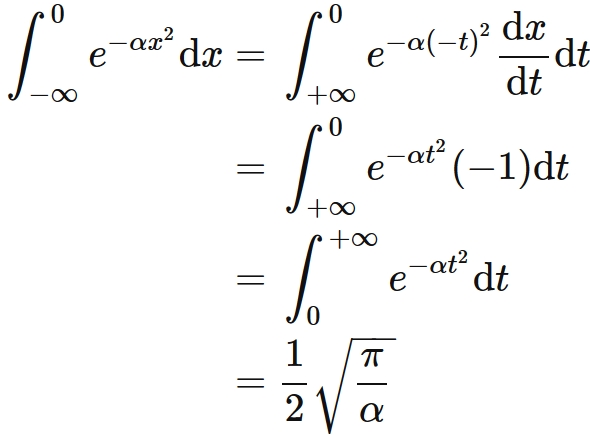



Gaussian Integral Formula And Proof Semath Info




Indefinite Integral Of 1 X Antiderivative Of 1 X Video Khan Academy




Ex 7 6 21 Integrate E 2x Sin X Using Integration By Parts
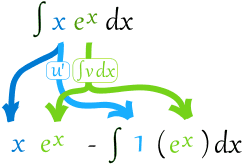



分部积分法




Ex 7 2 Integrate E 2x E 2x E 2x E 2x Ex 7 2



1
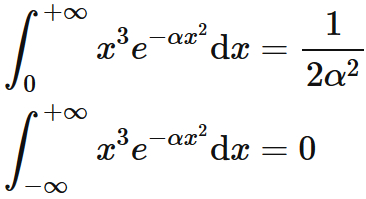



Gaussian Integral Formula And Proof Semath Info




X找到积分 Ex 2找到积分 积分x的结果会怎样 365最新备用网址 Bet365手机客户端首页




X 2 E X 2 X 2 Dx用于积分 365结算错误我又投注了 365bet平台赌场




積分 1 Sqrt E X 1 Youtube



How To Integrate X Sqrt X 2 Y 2 With An Order Dxdy Quora




Evaluate Int E X X 3 X 1 1 X 2 3 2 Dx



E的x次方积分 万图壁纸网




E的负x平方的积分 在线图书馆
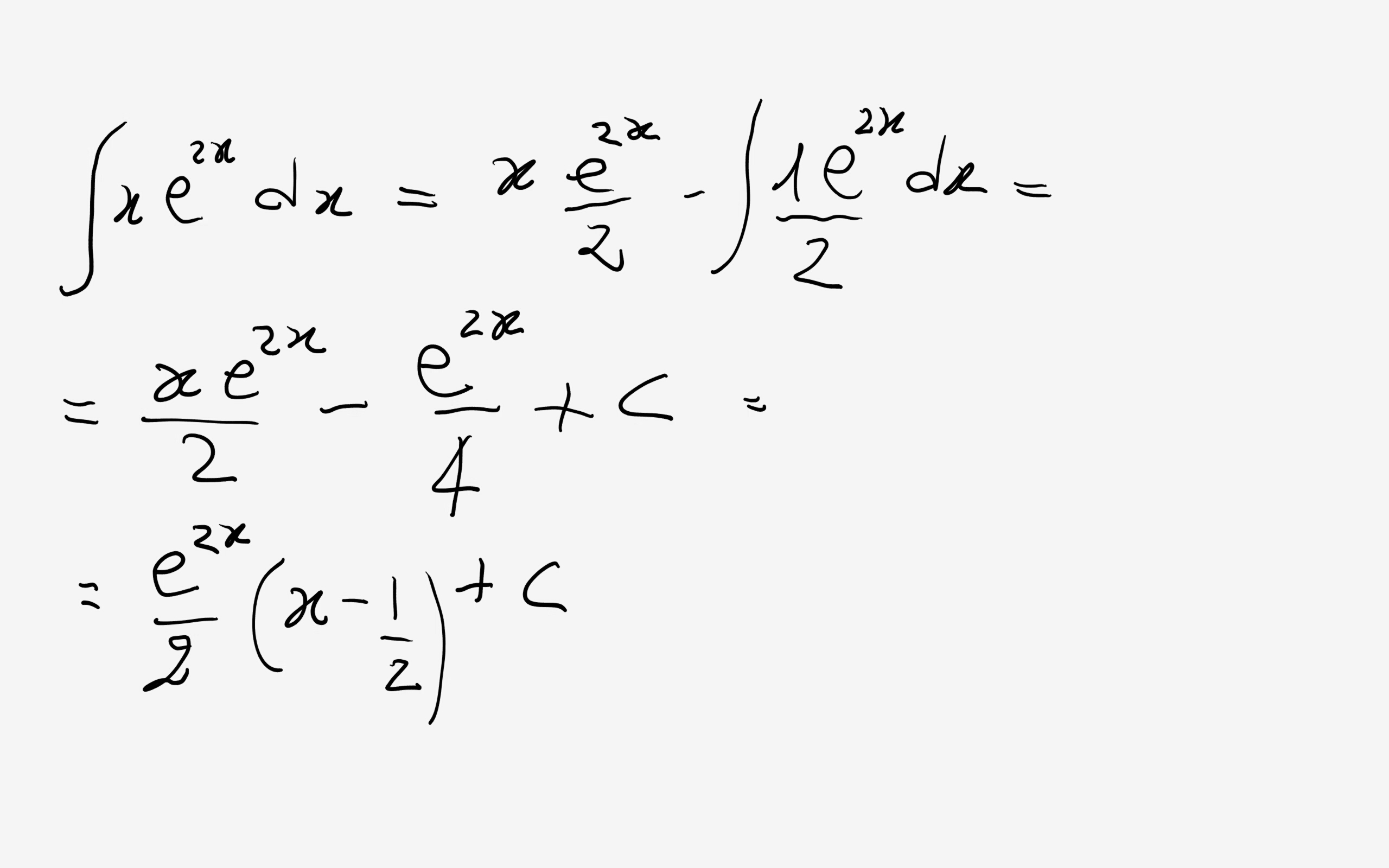



How Do You Integrate Xe 2x Dx Socratic
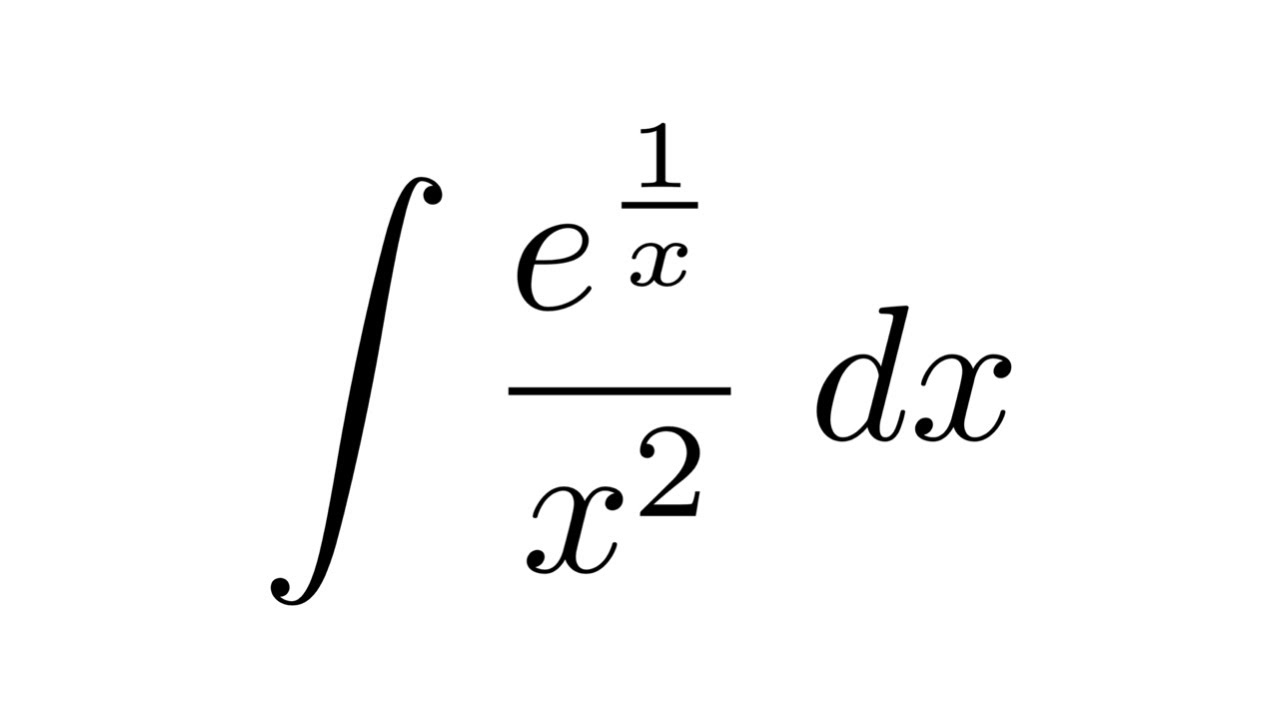



Integral Of E 1 X X 2 Substitution Youtube
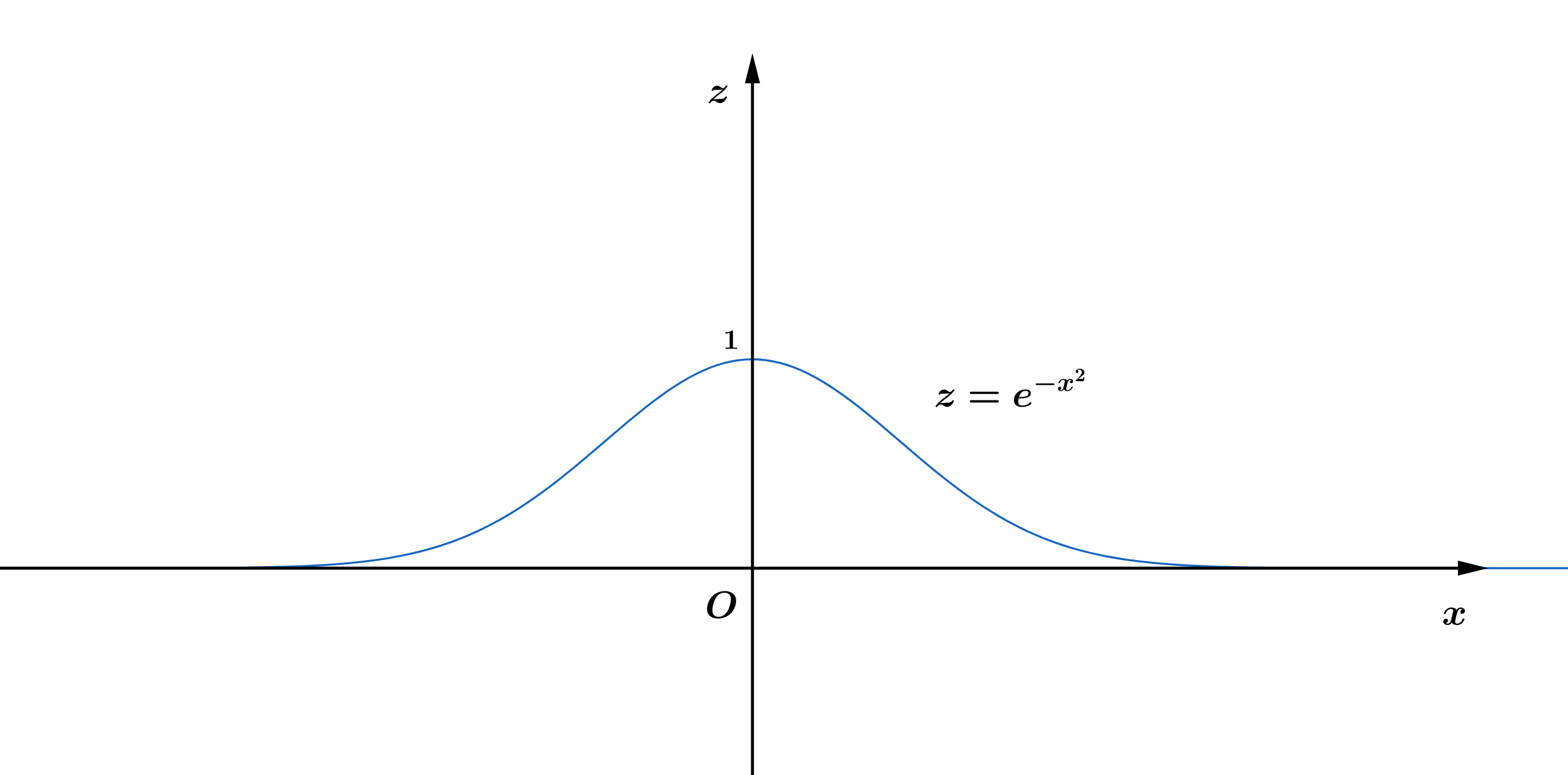



无穷积分 E X 2 Dx 的几种巧妙解法 Blogs Of Zcy1221 Csdn博客




What Is The Integration Of 1 Xe X Quora
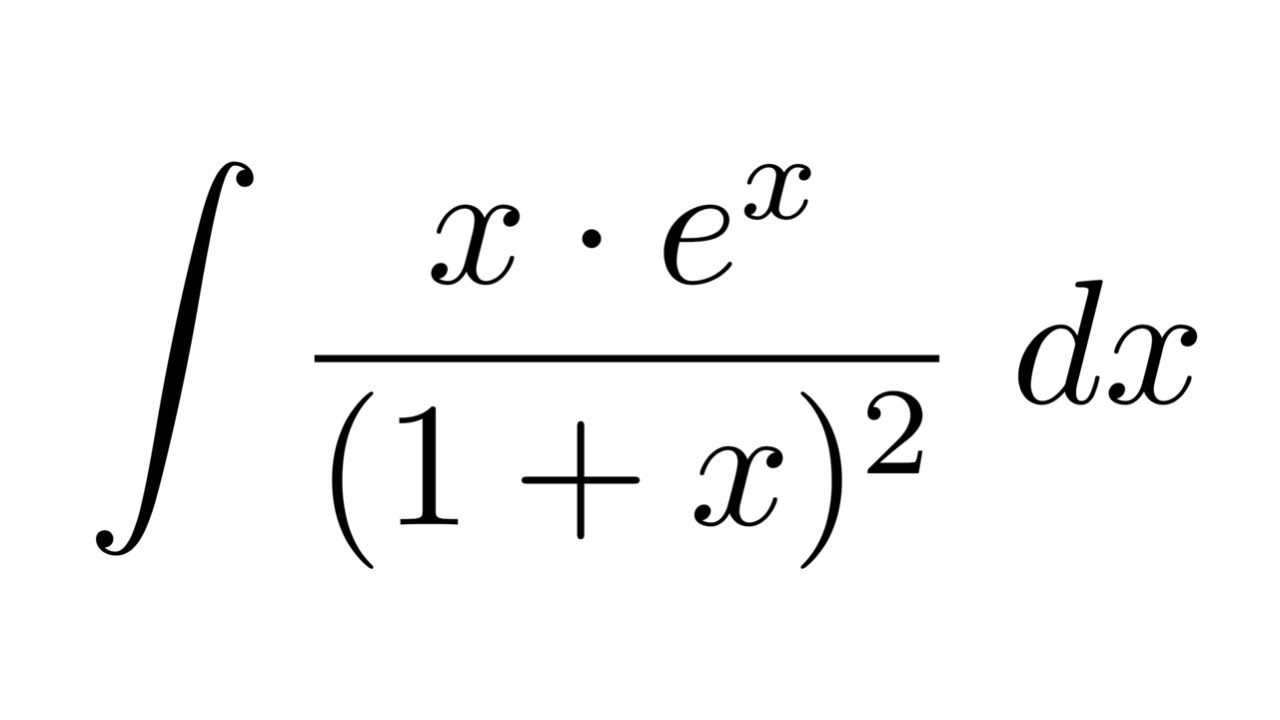



Integral Of X E X 1 X 2 By Parts Youtube




如何计算e的 X的平方 次方的不定积分 知乎




E的x次方积分 在线图书馆



求不定积分s Xe X Sqrt E X 2 Dx 数学竞赛平台 数学帮 Math110




Ex 7 6 21 Integrate E 2x Sin X Using Integration By Parts




Ex 7 2 Integrate E 2x E 2x E 2x E 2x Ex 7 2




ガウス積分の公式集 証明付 理数アラカルト




ガウス積分




Integrating E X 2 The Gaussian Integral Youtube




ガウス積分について宇宙一わかりやすく解説する 物理学生エンジニア




高斯積分 積分e X 2 中文版 Gaussian Integral Integral Of E X 2 Youtube



以下计算积分 X E X 2 Dx 的过程错在何处 知乎



Search Q E 2 E7 8d E5 86 Tbm Isch
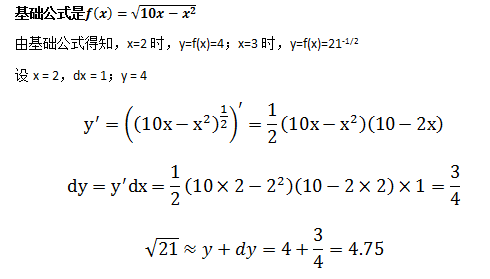



单变量微积分笔记11 微分和不定积分 我是8位的 博客园




Integration By Parts Wikipedia
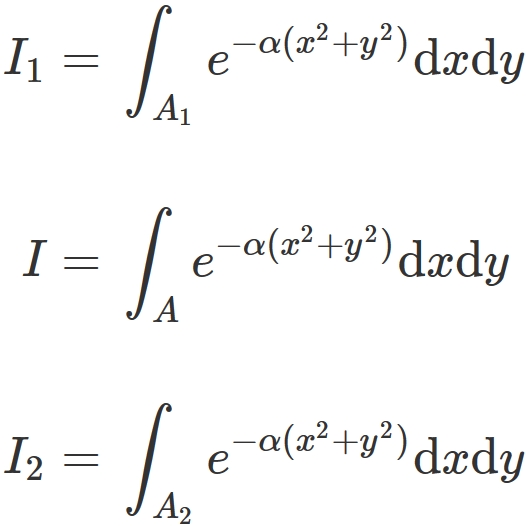



Gaussian Integral Formula And Proof Semath Info




求无穷积分 求e X 0到正无穷的积分 三人行教育网 Www 3rxing Org
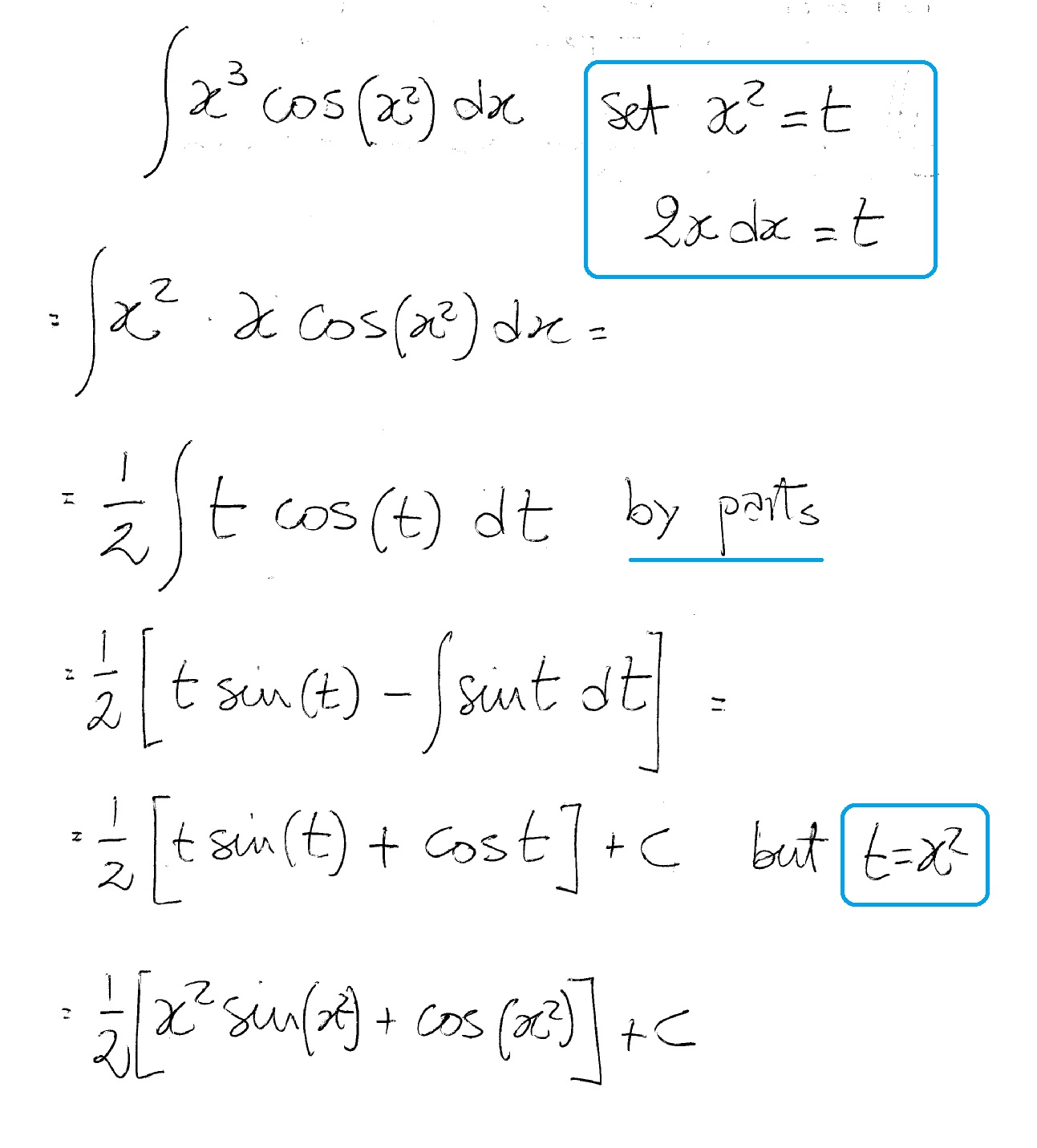



How Do You Integrate X 3cos X 2 Dx Socratic
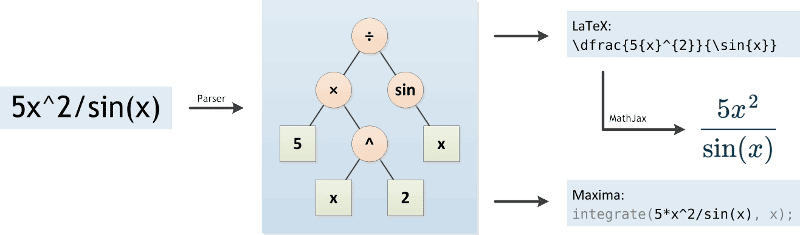



Integral Calculator With Steps




实验十用mathematica计算重积分



从 E X Sinxdx出发 积分随想 I 知乎



置換積分でexp X 2 の積分を求めたいのですが T X 2としてもt Yahoo 知恵袋




广义积分 Exp X 2 Dx 从负无穷到正无穷 原函数似乎求不出来啊 怎么算 雨露学习互助



Http Tyr0 Chem Wsu Edu Kipeters Chem332 Resources Tableofusefulintegrals Pdf



估计下列各积分值 4 S 0 2 E X 2 X Dx 数学竞赛平台 数学帮 Math110




微积分学 不定积分 练习答案 维基教科书 自由的教学读本



What Is The Integral Of E F X Quora
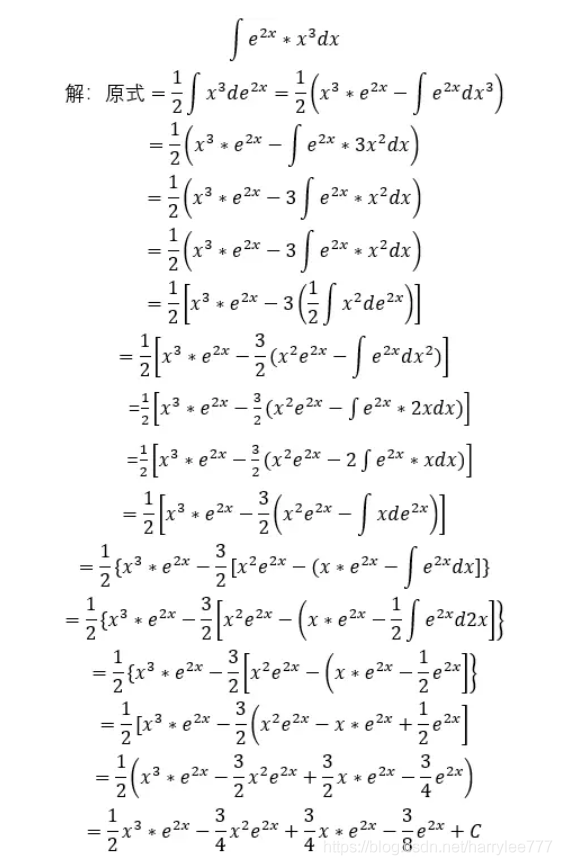



表格 列表法之分部积分 Harrylee777的博客 Csdn博客 表格法求分部积分



计算二重积分ss D E X 2dxdy 其中区域d是第一象限中由曲线y X 3及曲线y X所围成的区域数学竞赛平台




微积分学 不定积分 练习答案 维基教科书 自由的教学读本



E X 2 Dx的三种方法 知乎




求不定积分 1 二次根号下 E的x次方加二 雨露学习互助




无穷积分求 E X 2 在0到正无穷的积分求过程 三人行教育网 Www 3rxing Org



急求数学帝解答exp X 1 Exp 2x 积分过程我知道答案是atan 1 Exp X 1 Exp X 但是自己积分怎么就积分 不出来呢 我是令t Exp X 然后化成1 T 2 1 1 T 2 积分 但是这样的结果是 Exp 1 Arctan Exp X 作业 慧海网




E的x次方定积分x乘以e的负x次方 定积分
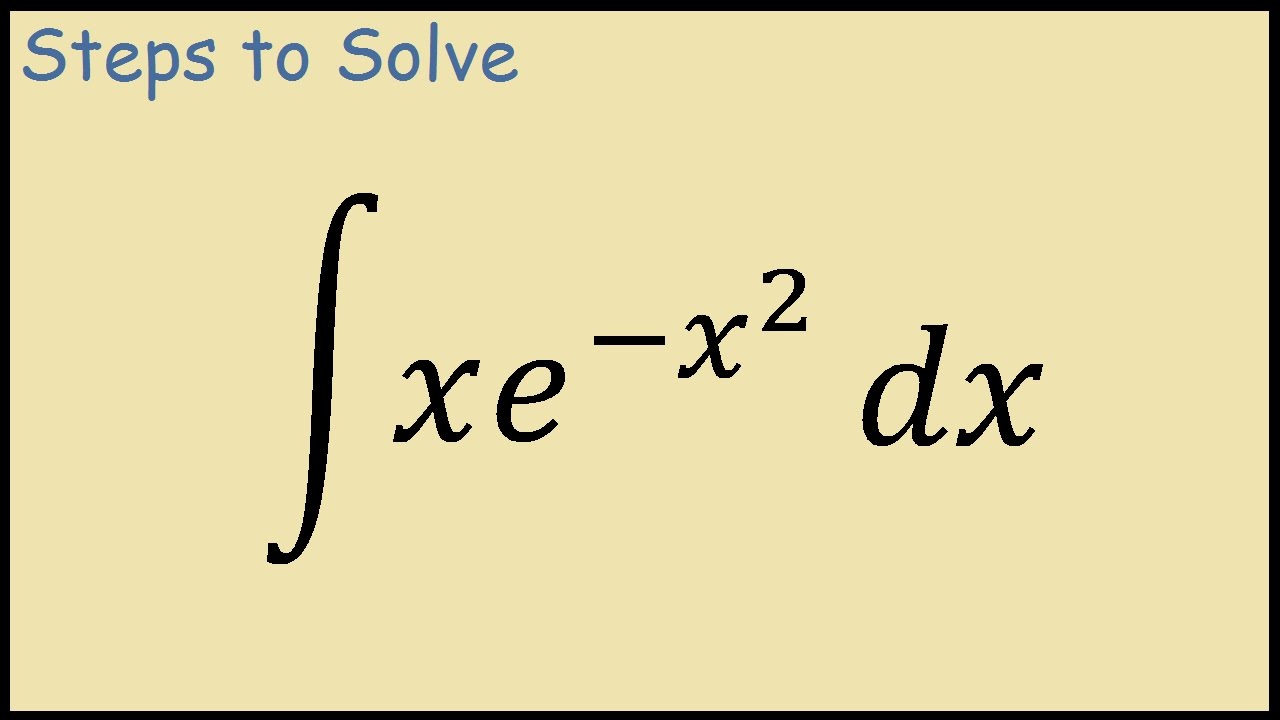



How To Integrate Xe X 2 Youtube



求不定积分s Xe X E X 1 2 Dx 数学竞赛平台 数学帮 Math110




Gaussian Integral Wikipedia



Dp0advswdfuxrm



以下计算积分 X E X 2 Dx 的过程错在何处 知乎



E 2x 積分 達人專欄 Uvyo




Int 1 Sqrt A 2 X 2 Dx Log X Sqrt X 2 A 2 C




超越函数e X 2 的定积分 Norstc的博客 Csdn博客
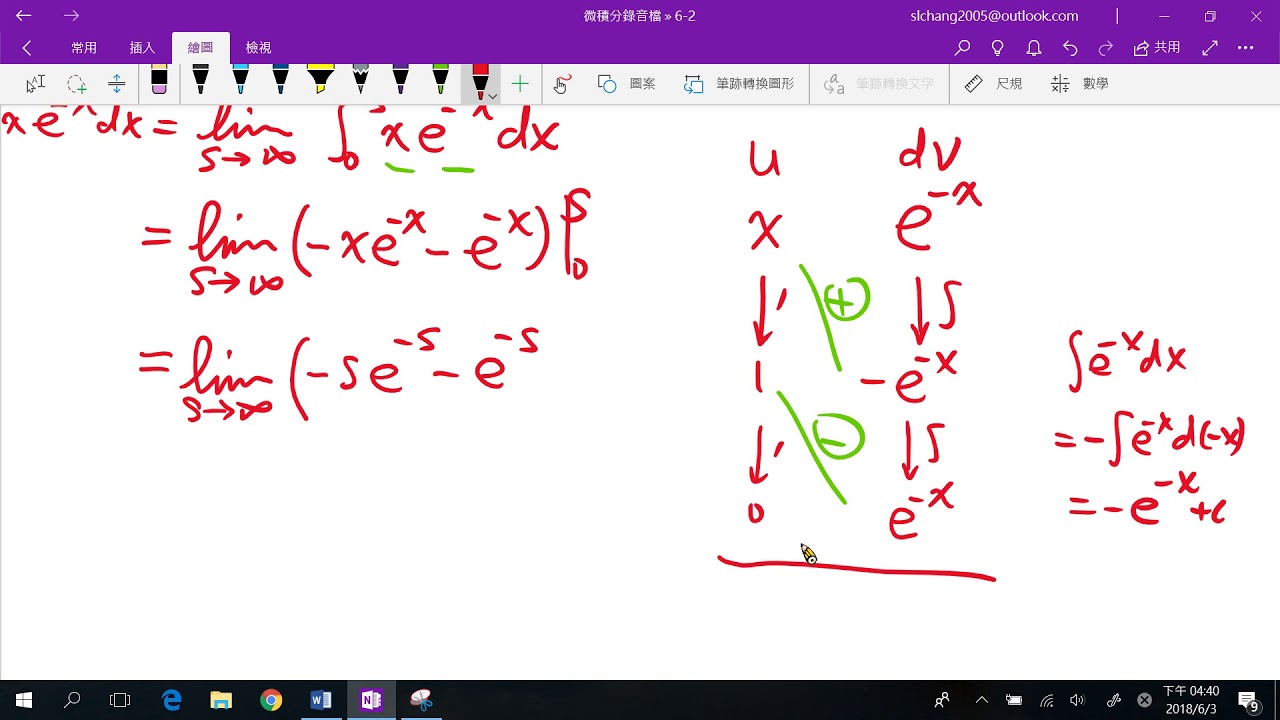



6 2 5 3 瑕積分int 0 Infty Xe X Dx Youtube




高斯积分 积分e X 2 从负无穷到正无穷 哔哩哔哩 Bilibili
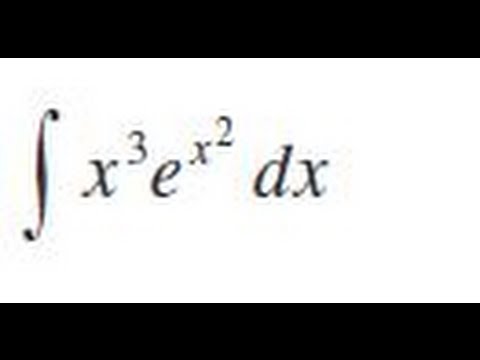



Integrate X 3 E X 2 Dx Youtube
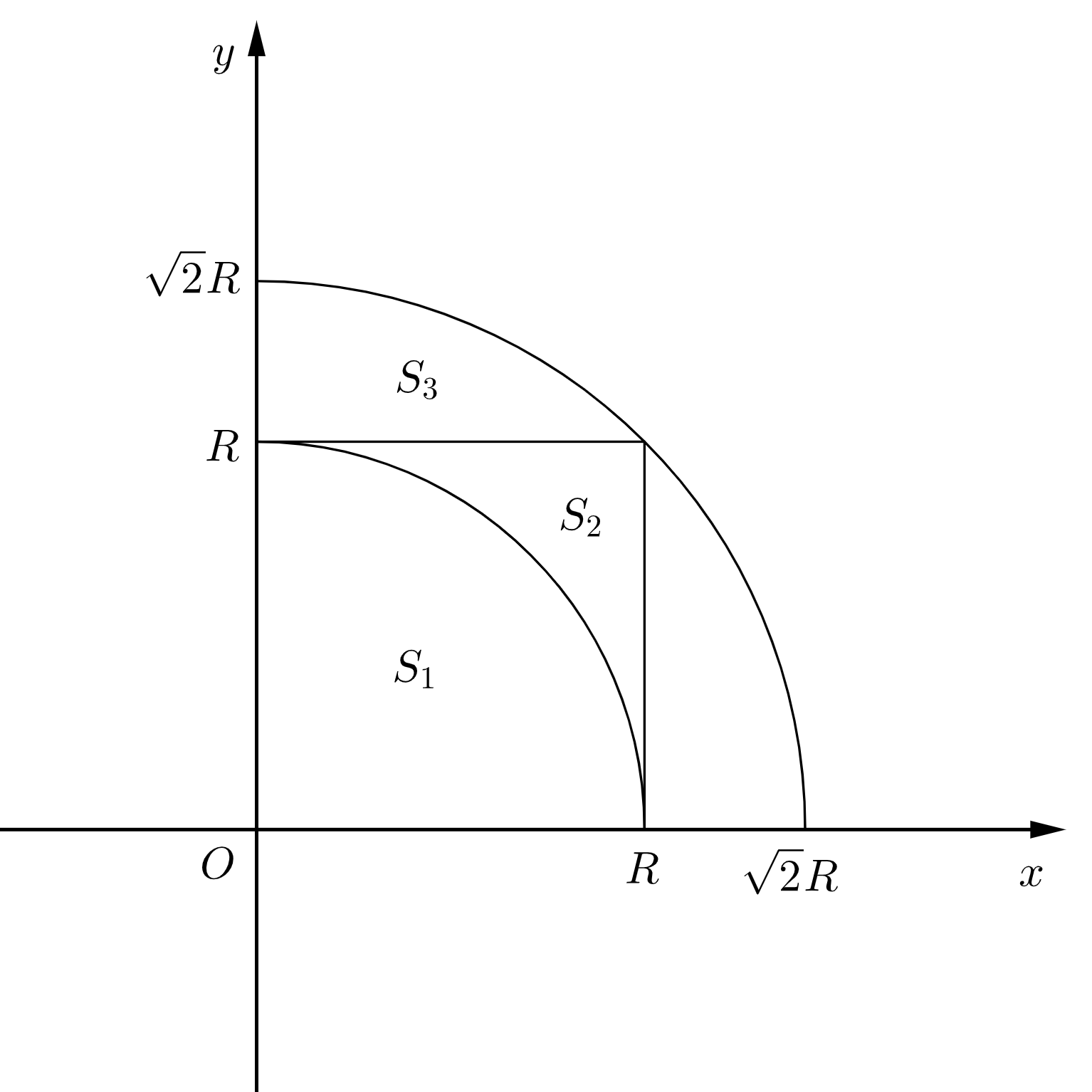



无穷积分 E X 2 Dx 的几种巧妙解法 Blogs Of Zcy1221 Csdn博客




Sym Py Edu




Gaussian Integral Wikipedia




高斯积分 维基百科 自由的百科全书



标签高斯积分下的文章 Joyful Physics




Dirichlet Integral Wikipedia




ガウス積分の公式集 証明付 理数アラカルト
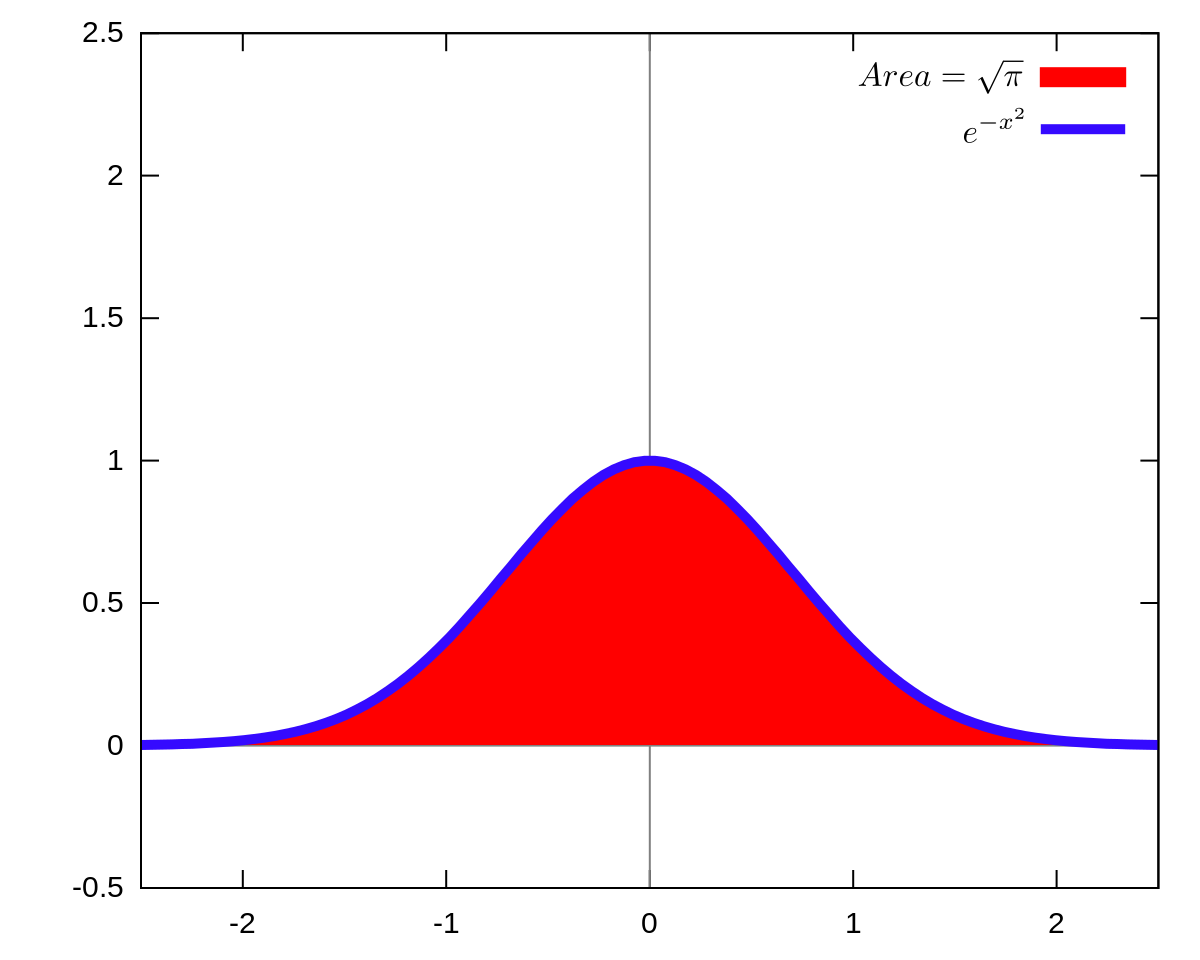



Gaussian Integral Wikipedia


コメント
コメントを投稿